Order Fractions Your Last Practice Accuracy 18 of 20 Gaberial You Can Practice Again or Test

Introduction

As the joke goes, "3 out of two people have trouble with fractions." Fractions accept been known from ancient civilizations until current times, but they still pose major problems when learning mathematics. Babylonian civilisation and Egyptians of 4000 years ago already worked with fractions. The processing of fractions is office of our everyday life and is used in situations such as the estimation of rebates, following a recipe or reading a map. Moreover, fractions play a key role in mathematics, since they are involved in probabilistic, proportional and algebraic reasoning. Then why is information technology so difficult for pupils to learn and stand for fractions? Fractions accept been used for centuries and are manipulated in a bully variety of everyday life situations and in mathematics, and yet they are hard for students to grasp and master. In this commodity, we will endeavor to shed light on children's difficulties when they learn fractions.

Fractions are well-known to constitute a stumbling block for primary schoolhouse children (Behr et al., 1983; Moss and Case, 1999; Grégoire and Meert, 2005; Charalambous and Pitta-Pantazi, 2007). Agreement difficulties in learning fractions seems absolutely crucial equally they can lead to mathematics anxiety, and touch on opportunities for further date in mathematics and scientific discipline. Various hypotheses have been proposed in order to explain those difficulties. In this inquiry, we used a theoretical framework based on psychological and educational theories to define problems encountered by pupils when they learn fractions. We tested iv^th, 5^th, and 6^th-graders in guild to identify children'south difficulties more precisely.

Dissimilar Obstacles in Learning Fraction

Whole number bias

Fractions are rational numbers. A rational number tin be divers equally a number expressed by the quotient a/b of integers, where the denominator, b, is not-zero. According to a recent theory of numerical development, children who have not nonetheless learned fractions generally believe that the properties of whole numbers are the same for all numbers (Siegler et al., 2011). Indeed, one of the main difficulties when learning fractions comes from the utilize of natural number backdrop to brand inferences on rational numbers, what Ni and Zhou (2005) chosen the "whole numbers bias." This bias leads to difficulties conceptualizing whole numbers every bit decomposable units.

From a mathematical viewpoint, there are fundamental differences betwixt those 2 types of numbers. Firstly, rational numbers are a densely ordered set, whereas whole numbers class a discrete gear up. Between two rational numbers, there is an infinity of other rational numbers, while between ii natural numbers, at that place is no other natural number (Vamvakoussi and Vosniadou, 2004). Secondly, some other feature of rational numbers is the possibility to write them from an infinity of fractions. This corresponds to the notion of equivalent fractions. Thirdly, faction symbols are a/b types. Pupils frequently process numerator and denominator as 2 carve up whole numbers (Pitkethly and Hunting, 1996). They apply procedures that can only be used with whole numbers (Nunes and Bryant, 1996). Consequently, typical errors announced in addition or subtraction tasks (e.g., 1/4 + 1/2 = 2/6), and also in fraction comparison (due east.grand., ane/v >ane/iii). In this case, pupils' reasoning can exist resumed as follows: if the number is larger, then the magnitude it represents is larger. But when nosotros recollect virtually fractions, a larger denominator does not hateful a larger magnitude, but a smaller one. Another difficulty appears in multiplication tasks. Multiplying natural numbers always lead to a larger answer, merely information technology is non the case with fractions (east.thousand., 8 × ane/iv = 2).

The inappropriate generalization of the knowledge nigh natural numbers is fifty-fifty more resistant as it is widely anterior to the one near rational numbers (Vamvakoussi and Vosniadou, 2004). In society to overcome these mistakes, it would seem necessary for students to perform a conceptual reorganisation which integrates rational numbers as a new category of numbers, with their own rules and functioning (Stafylidou and Vosniadou, 2004). Furthermore, even in adults, knowledge about natural numbers is often preponderant when processing fractions (Bonato et al., 2007; Kallai and Tzelgov, 2009).

Different meanings of fractions

Another major difficulty comes from the multifaceted notion of fractions (Kieren, 1993; Brousseau et al., 2004; Grégoire and Meert, 2005). Kieren (1976) was the get-go to divide fractions into 4 interrelated categories: ratio; operator; quotient; and measure out. The ratio category expresses the notion of a comparison betwixt two quantities, for example when there are three boys for every four girls in a group. So in this example, the ratio of boys to girls is iii:iv; the boys representing three/7 of the group and the girls four/7 of the group. In the operator category, fractions are considered as functions applied to objects, numbers or sets (Behr et al., 1983). The fraction operator tin can enlarge or shrink a quantity to a new value. For instance, finding three/4 of a number tin can be a function where the functioning is multiply past iii divided past 4, or divided by 4 and and so multiply by 3. The quotient category refers to the result of a division. For example, the fraction iii/4 may be considered as a quotient, 3/4. In the measure out category, fractions are associated with two interrelated notions. Firstly, they are considered equally numbers, which convey how big the fractions are. Secondly, they are associated with the measure of an interval. According to Kieren (1976), the part-whole notion of fractions is implicated in these four categories. That is the reason why he did not describe it every bit a 5th category.

Thereafter, Behr et al. (1983) proposed a theoretical model linking the dissimilar categories of fractions. They recommend considering part-whole equally an additional category. They also associated sectionalisation to the part-whole notion. The part-whole category can then be defined every bit a situation in which a continuous quantity is partitioned into equal size (e.g., dividing a cake into equal parts), and partitioning would exist the same with a ready of discrete objects (e.yard., distributing the same amount of sweets among a group of children).

Other models have been proposed to draw the multiple meanings of fractions (Brissiaud, 1998; Rouche, 1998; Mamede et al., 2005). These models partly overlap, but are not entirely equivalent. For instance, Mamede et al. (2005) present four types of fraction utilize: quantifying a part-whole relationship, quantifying a quotient, representing an operator, representing a relation between quantities. Meanwhile Grégoire (2008) suggests a different model, in which three categories correspond to three conquering stages. In the outset stage, the fraction is seen as an operator. This notion refers to sharing situations. The 2nd one is the ratio stage which requires a loftier level of abstraction because ane needs to sympathize that different fractions can represent the same ratio. This is linked to the notion of equivalent fractions. The third and concluding stage is related to the numerical meaning of fractions. Fractions are hither conceived equally a new category of numbers, with their ain rules and properties.

Conceptual and procedural understanding

Another caption of children'southward difficulties when learning fractions lies in the articulation between conceptual and procedural noesis. Previous studies have shown that children would often perform calculations without knowing why (Kerslake, 1986).

Conceptual knowledge tin can be defined as the explicit or implicit agreement of the principles ruling a domain and the interrelations between the different parts of knowledge in a domain (Rittle-Johnson and Alibali, 1999). Information technology tin too be considered equally the knowledge of key concepts and principles, and their interrelations in a particular domain (Schneider and Stern, 2005). Conceptual cognition is thought to be mentally stored in a form of relational representations, such as semantic networks (Hiebert, 1986). It is not tied to a specific problem, but tin can exist generalized to a grade of problems (Hiebert, 1986; Schneider and Stern, 2010).

Procedural knowledge can exist defined as sequences of actions that are useful to solve problems (Rittle-Johnson and Alibali, 1999). Some authors consider procedural noesis every bit the knowledge of symbolic representations, algorithms, and rules (Byrnes and Wasik, 1991). Moreover, procedural noesis would allow people to solve bug in a quick and constructive way equally it tin can easily be automatized (Schneider and Stern, 2010). Therefore, it can be used with few cognitive resources (Schneider and Stern, 2010). However, procedural cognition is non as flexible every bit conceptual knowledge and is ofttimes leap to specific trouble types (Baroody, 2003).

Those 2 types of knowledge may not evolve in independent ways. Many theories on knowledge acquisition suggest that the generation of procedures is based on conceptual understanding (Halford, 1993; Gelman and Williams, 1997). They argue that children use their conceptual understanding to develop their discovery procedures and adapt acquired procedures to new tasks. According to this approach, children's difficulties when learning well-nigh fractions could be interpreted as a apply of mathematical symbols without access to their meaning. Procedural knowledge may also influence conceptual understanding. Using procedures would pb to a meliorate conceptual agreement. Simply few studies back up this thought. For instance, Byrnes and Wasik (1991) argue that many children acquire the correct procedures to multiply fractions, but they never seem to empathise the underlying principles. Other authors support a tertiary bespeak of view. Both types of knowledge might progress in an iterative and interactive way (Rittle-Johnson et al., 2001). Conceptual and procedural cognition might continually and incrementally stimulate each other. Neither would necessarily precede the other.

In mathematics education, teachers seem to focus more than on procedural than conceptual noesis. Children usually learn rote procedures in a repetitive way. This leads to a misunderstanding of mathematical symbols (Byrnes and Wasik, 1991). Consequently many computational errors are due to an impoverished conceptual agreement.

Our Theoretical Framework

Taking into account the different theoretical models presented and the problems they ascend led us to build our ain conceptual framework. In this study exploring the difficulties in learning fractions, two primary components were considered: a conceptual component and a procedural component.

The conceptual component was divided in iv distinct aspects: proportion, number, measure and office-whole/division. Part-whole/partitioning refers to how much of an object (e.m., 1/2 pizza) or a collection (e.g., 1/2 of a bag of sweets) is represented past the fraction symbol (Hecht et al., 2003; Kieren, 1988). Typical tasks used to assess that kind of conceptual knowledge involve shading parts of a figure indicated by a fraction, or the contrary practise consisting of writing the fraction representing the quantity of a figure that is shaded (Hiebert and Lefevre, 1986; Byrnes and Wasik, 1991; Ni, 2001). Proportion represents the comparison between 2 quantities. We used comparing of different expressions of the same ratio (e.g., 1/ii, 2/4, and 3/?) as it is an adequate way to appraise the understanding of proportion. The numerical meaning of fraction refers to the fact that fractions represent rational numbers that can be ordered on a number line (Kieren, 1988). Two relevant tasks were used to appraise children's agreement of the numerical pregnant of fractions: firstly, number lines on which they are asked to place a fraction, and secondly, indicating which of several given fractions represents the largest quantity (Byrnes and Wasik, 1991; Ni, 2000).

Several variables also held our attention regarding the representation of fractions. Discrete and continuous quantities were used. Children might have greater difficulties to link 2/iv to 2 out iv for elements of a gear up than ii/iv of a pie (Ni, 2001). Multiple objects and figures, as well equally numerical symbols were introduced to assess the possible interference of certain types of representations (Coquin-Viennot and Camos, 2006). For practical reasons, nosotros did not examine fractions as a measure in this written report. This category is closely related to the metric organisation. The manipulation of fractions as a measure tin can be made by splitting units of length, surface area, book, time, mass, etc. Understanding these measuring situations involves several concepts that are non exclusively related to fractions, such equally understanding different unit systems or a practiced grasp of the decimal position arrangement. Therefore, it is difficult to assess the understanding of this category in isolation from these variables.

Procedural items were those that could be easily solved past applying a process that could exist implemented without checking for meaning outside that particular procedure. The procedural component involved various operations on fractions, namely the addition and subtraction with or without common denominators, multiplication, and simplification of fractions. Children were given unlike arithmetical operations to solve likewise as simplification exercises.

Enquiry Questions

The master aim of this study was to provide empirical data that could explain difficulties encountered by children when they acquire fractions. Our first objective was to analyse the mathematics curriculum of the French Community of Kingdom of belgium, where this study was conducted. Our 2d objective was to understand the nature of pupils' difficulties through different categories.

Nosotros addressed several research questions regarding children's difficulties when learning fraction. First, we wanted to define more precisely the difficulties encountered by main schoolhouse children. 2d, ane of the goals of this study was to clarify the relationship betwixt conceptual and procedural cognition of fractions. Does conceptual knowledge of fractions influence procedural knowledge? Or is procedural knowledge sufficient to understand fractions? Our hypothesis is that children's difficulties come from a lack of conceptual understanding of fractions. Their errors would come up from the application of routine procedures, but they do not empathize the diverse underlying concepts.

Conceptual knowledge of fractions was assessed through tests about the different meanings of fractions (role-whole, proportion, number), and the different representations of fractions (eastward.g., association betwixt figural, numeral, and verbal representations). Procedural cognition about fractions was evaluated through operations on fractions and simplification tasks.

Methods

Participants

The test was administered to eight Form 4 classes (hateful age: nine years 11 months old), 8 Grade v (mean historic period: eleven years 1 calendar month former) classes and viii Grade 6 classes (mean historic period: 12 years old) from 5 unlike schools, representing a total sample of 439 participants (214 girls and 225 boys). The pick of these grades was deliberate, every bit fraction learning usually starts from Grade iv in the French Community of Belgium where the written report was conducted. Informed consent was obtained from parents and the managing director of every school, too as from the 24 teachers involved in this research. Assent from children was obtained at the onset of both testing sessions.

The Setting of the Written report

We analyzed 21 mathematics textbooks recognized by the Educational activity Department of the French Community of Belgium. Fraction concepts used in mathematics textbooks in Grade 4–6 were listed. The goal was to analyse the progression of fraction learning proposed by those textbooks. The about hit ascertainment was that there was a great variety of ways to introduce fractions. In well-nigh textbooks, the part-whole concept was considered every bit the starting point, merely in some cases, the measure out concept was introduced first. Every concept described in our theoretical framework was represented in the textbooks, but the number of exercises apropos each ane of them varied greatly.

We besides examined the official mathematics program of the French Community of Belgium. The program presents, in a structured fashion, the bones skills for the first 8 years of compulsory educational activity, and the skills pupils have to master by the end of each stage (Ministère de la Communauté française, 1999). Fractions were divided into two different categories, Numbers and Quantities. Whatever requirement at the end of master school (Course 6) is briefly reviewed in this section. In the Number category, pupils should be able count, enumerate and classify fractions as well every bit decimal numbers. They should besides be able to summate, identify and solve operations involving fractions and decimal numbers. In the Quantities category, children are supposed to operate and fractionate different quantities in order to compare them. They should be able to add together upwardly and subtract 2 fractions every bit well equally calculating percentages. The plan likewise mentioned their ability to solve proportionality problems.

The official program offers a list of what pupils should know about fractions in chief school. But what did not appear clearly was a logical progression between all the meanings of fractions. For example, how and when should equivalent fractions be introduced? At that place was not a clear evolution for teaching fraction. This situation may be risky as teachers might present fractions as a succession of different independent activities with no real underlying logical progression.

In guild to complete the information found in the textbooks, we analyzed pedagogical practices about the fashion teachers introduce and teach fractions. This investigation revealed the not bad multifariousness of ways to teach fractions. Our analysis was based on different sources. Firstly, nosotros asked the 24 teachers involved in this written report to requite united states of america a listing of all the activities about fractions conducted in their classrooms. Secondly, teachers gave u.s.a. a sample of their lessons on fractions also as pupils notebooks. Thirdly, we fabricated informal observations during the tests.

In Class 4, pupils learn how to read and stand for the value of a fraction. They beginning placing fractions on a graduated number line. They learn how to simplify fractions (i.e., introduction to equivalent fractions). They acquire how to add together and decrease of fractions with small and mutual denominators. In Grade 5, children learn more most fractions as numbers and how they correspond quantities. Pupils are trained to catechumen fractions into decimal numbers and vice versa. They utilize addition and subtraction of fractions with different denominators. Improper fractions are introduced. In Course 6, multiplication of fractions is introduced.

Our assay highlighted the fact that teachers are more inclined to use procedures than what is recommended by the official plan. The dissimilar conceptual meanings are presented successively without any logical progression. The club in which they are introduced depends on the teacher and on the textbook used by the teacher. Furthermore, fractions seem isolated from mathematics lessons and are taught similar a divide topic.

Test

A test was designed to answer our research questions. Its construction has been guided past our theoretical framework likewise as the main school curriculum in the French Customs of Belgium. The test was split into 2 parts. Office A was made of xix questions, Role B of 20 questions. There were ane to eight items for each question. There were 46 items in Part A and 48 in Part B. Function B was administered one calendar week after Part A. Pupils had fifty min to answer each part.

Conceptual knowledge assessment

Conceptual knowledge of fractions was assessed through different categories of questions: office of a whole/partition, proportion and number. Three types of representations have been used: symbolic (e.chiliad., i/4), exact (e.1000., i-quarter) and figural representations (e.1000., a square where the colored function represented 1/4). Discrete and continuous quantities were used.

Multiple variables were taken into account regarding numerical and exact representations, such every bit the degree of familiarity, or the parity of the denominator and the numerator. The following variables were controlled regarding figural representations: the equivalence of the parts; the shape of the effigy (square, rectangle, triangle …); the size of the figure; and the contiguity of the colored parts of the figure.

Part-whole/sectionalization . Part-whole cess included items for which children had to link fractions to a figural representation. The get-go question consisted of 6 items for which children were asked to represent a given fraction with a effigy (e.g., draw a figure representing i/7). The items were familiar fractions (ane/2 and three/four), unfamiliar fractions (1/7 and iv/five) and improper fractions (i.east., fractions larger than i; 3/2 and vii/five). In the second question, pupils were asked to choose a figure representing a given fraction (e.grand., choose figures representing ane/4, see Appendix). In the tertiary question, they were asked to shade a certain portion of a figure. In that location were four items for this question. In the first two items, children were asked to shade 3/4 of a square or a rectangle. In the next 2 items, they were asked to shade iv/v of a pentagon or a foursquare.

Proportion . For questions about proportion, children were asked to compare quantities based on the rule of three. 5 quantities were given in a table and they had to give the sixth quantity. There were verbal representations, such as "3 cakes cost €six, 5 cakes cost €10, 7 cakes price €?" There were also figural representations. An example of figural representation is given in Figure one. The contextualization of the items was introduced to make sure that children based their answer on both columns of the tables.

Figure ane. Case of a figural proportion item.

Numbers . For the number category, there were four types of questions. The showtime question was a comparison of fractions. Pupils had to decide which of two fractions represented the larger quantity. At that place were fractions with the same numerator (e.g., two/3_2/7), fractions with the same denominator (due east.g., 3/8_5/eight) and fractions with no common components (e.g., ii/5_1/iv). In the second question, pupils were asked put fractions in ascending order. This question as well involved improper fractions and natural numbers. The given numbers were the following: 3/iv, 1/2, 8/iv, and 1. The third question involved finding a fraction between 2 given fractions (east.g., find a fraction between 2/7 and 5/vii). Fractions with mutual denominators, common numerators, and no common components were included. For the fourth question, pupils were asked to identify a fraction or the unit on a graduated number line (east.g., given 0 and 1/4, place 3/four on the number line). The given references were always 0 and another fraction.

Procedural noesis assessment

Nosotros assessed the post-obit procedures: addition and subtraction with or without the same denominator; multiplication of fractions; multiplication of a fraction by an integer; and simplification of fractions. Those procedures were assessed with typical questions such as 1/2 + 1/4 = ?. Division of fractions was not included equally information technology is non role of the official curriculum.

Results

General Results

Descriptive statistics are reported for each category of fractions (part-whole, proportion, numbers, operations, and simplification). Hateful scores and standard deviations are e'er expressed in percentage. Equally can be seen in Table ane, children performed meliorate for questions about proportion and function-whole than for questions virtually the other categories. There were however major difficulties in Grade 6 for the part-whole category. Indeed, even in Grade 6, the percentage of correct responses was nonetheless far from ceiling performance. Children were capable of resolving questions on proportional reasoning from Course four. The principal observed errors were linked to additive reasoning. Children got the lower scores in Grade 4 for arithmetic operations. This was not surprising as learning about operations on fractions usually offset in Grade five.

Table 1. Mean pct of correct responses and standard deviation for each category in Grade 4–six.

A correlation analysis was run to assess the relations betwixt conceptual (part of a whole, proportion and numbers) and procedural categories (operations and simplification). The correlation assay revealed that conceptual categories correlated significantly with each other (run into Table ii). They also correlated positively with procedural categories.

Table 2. Correlations between conceptual items and procedural items.

We ran an ANOVA for repeated measures with category as a within-subjects factor (function-whole; proportion; number; operations; simplification) and grade as a between-subjects cistron. There was a meaning course consequence, F _{(2, 437)} = 71.53, p < 0.001, ηⁱⁱ _p = 0.25. There was too a principal effect of category, F _{(four, 1744)} = 242.64, p < 0.001, η² _p = 0.36, and a significant grade x category interaction, F _{(8, 1744)} = 19.85, p < 0.001, η^two _p = 0.08 (see Effigy 2A). Tukey post-hoc tests showed that accuracy for operations and simplification was poorer in Grade 4 than in Grades 5 and half dozen (p < 0.001).

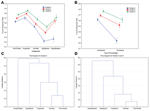
Figure 2. The summit two panels show the interaction betwixt course and correct response rates for each category (A), and between grade and each blazon of knowledge (B). Vertical bars denote 95% confidence intervals. The bottom two panels bear witness dendrograms depicting the results of a single linkage hierarchical clustering of each category based on Euclidian distances for Grade 4 (C) and Grades five and half-dozen (D).

We ran another ANOVA for repeated measures on the blazon of cognition (conceptual and procedural) with grade as a betwixt-subjects factor. In that location was a meaning effect of grade, F _{(2, 437)} = 75.23, p < 0.001, η² _p = 0.26. At that place was too a significant consequence of the type of knowledge, F _{(1, 438)} = 459.5, p < 0.001, η² _p = 0.51, and a significant grade 10 blazon of knowledge interaction, F _{(2, 437)} = 242.64, p < 0.001, η^two _p = 0.36 (see Figure 2B). Tukey post-hoc examination was used to decide pregnant differences betwixt class hateful values for each type of cognition, revealing that performance was poorer for procedural noesis in Form four than in Grades 5 and 6 (p < 0.001).

We likewise ran cluster analyses to ensure that our categories reflected conceptual and procedural knowledge. Since two patterns appeared in the results, we ran two split cluster analyses: ane assay for Course 4 and ane analysis for Grades 5 and 6. We ran neighbor-joining analyses (single linkage method) to meet if our categories formed natural clusters that could be labeled according to a type of noesis. These analyses provide a tree-structured graph (i.east., dendrogram) that is used to visualize the results of hierarchical clustering calculations. The dendrogram indicates at what level of similarity whatever 2 clusters were joined. It was constructed using neighbour-joining algorithm based on Euclidian distances. Both for Class 4 and for Grades 5 and 6, the dendrograms amassed the categories into 2 distinct groups that represent to our two types of knowledge, i.due east., conceptual and procedural (see Figures 2C,D). Office-whole, number and proportion were the nigh similar and stand for to our conceptual categories, whereas operations and simplification can exist combined in a dissimilar cluster, that is our procedural categories.

Part-Whole/Partition

Draw a representation for each given fraction

Table 3 shows hateful scores and standard deviation for the start question related to the part- whole/sectionalisation pregnant of fractions. Unlike variables were involved in this question. Firstly, an ANOVA with the blazon of fraction every bit inside-subject factor (2 levels: proper fraction vs. improper fraction) was run. Operation was worse for improper fractions than for proper fractions, F _{(1, 438)} = 2039.2, p < 0.001, η² _p = 0.90. Secondly, familiar (one/two, 3/4) and unfamiliar fractions (i/7, 4/5) were compared in another ANOVA. Performance for familiar fractions was significantly better than for unfamiliar fractions, F _{(one, 438)} = 2406.9, p < 0.001, η² _p = 0.92.

Table 3. Mean per centum and standard divergence for the question: Describe a representation of the given fraction.

Despite potential graphic difficulties, pupils more often than not divided a common continuous shape (circle or foursquare, run into Figure 3). 90% of pupils represented continuous quantities.

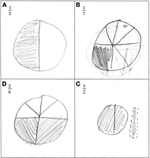
Effigy 3. Analogy of the most common answer when pupils were asked to draw a representation of a given fraction. 90% of them drew continuous quantities such as a circumvolve or a rectangle. In this item example, simply one/two was represented correctly (A). Parts of the drawings were unequal for one/7 and 2/6 (B and C). Different shapes were used for 3/2 (D).

Select the figures representing 1/4

In this task, pupils had to choose figures representing the quantity i/4 (encounter Appendix). Hateful percentage of correct responses were high in every grade (Hateful = 92% ± 6%). Simply when figures were representing 2/eight, we observed a dramatic drop of performance: 24 ± 6% in Grade 4, 29 ± eight% in Grade 5 and 59 ± 9% in Course 6. There was a significant difference between continuous and discrete quantities, F _{(1, 438)} = 2308.1, p < 0.001, η^two _p = 0.91. Performance was better for continuous quantities.

Shade a certain fraction of a figure

In this job, pupils had to shade three/4 or four/v of a given effigy. Mean scores per course are given in Tabular array 4. Hateful scores for 3/4 (Hateful = 83 ± 2%) were higher than for four/5 (Hateful = 65 ± 4%). An ANOVA with familiarity every bit a within-field of study cistron showed a significant difference betwixt 3/4 and iv/v, F _{(1, 438)} = 3156.6, p < 0.001, η ^two _p = 0.93.

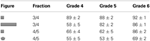
Table four. Mean scores and standard departure for each item in which pupils had to shade 3/iv or 4/5 of a given figure.

Proportion

As seen in Table i, performance for proportion items was better than in other categories. Withal, ten% of the answers given by iv^th-graders were based on additive reasoning. This pct dropped to v% in Grade v and 2.half-dozen% in Form 6. This type of error was more nowadays for numerical items (Form 4 = ix%; Grade 5 = seven%; Grade 6 = iii%) than for figural items (Class 4 = ii%; Grade 5 = ii%; Form 6 = 1%). A single-factor ANOVA was run and showed no significant difference between numerical and figural items, F _{(1, 438)} = 0.six, p = 0.eight.

Number

Place a given fraction on a number line

Percentage of correct responses showed a clear difference between three groups of items. In the first grouping of items, there were three number lines for which pupils only had to count the number of graduations corresponding to numerators to succeed (east.g., knowing 0 and 5/ix on the 5th graduation, identify two/9). For these items, they could but process the numerator and ignore the denominator. Mean percentage of correct responses for these items was 89 ± 6%. In the 2nd group of items, there were ii number lines on which pupils had to place 1 (e.g., knowing 0 and 1/5 on the first graduation, identify 1). The mean score for this group of items was the following: Mean = 40 ± 22%. The third grouping of items involved equivalent fractions (e.g., knowing 0 and 1/6 on the second graduation, place two/3). The mean score for these items was the following: Mean = 31 ± 24%. An ANOVA with the group of items every bit a within-field of study factor showed a significant deviation between the get-go group of items compared to unit items and items involving equivalent fractions, F _{(2, 437)} = 2942.6, p < 0. 001, ηⁱⁱ _p = 0.95. Tukey postal service-hoc tests showed that the first group of items was higher than unit items (p < 0.001) and equivalent fractions items (p < 0.001).

Error analysis showed that when asked to place 1 on a number line, pupils had a trend to place information technology at the beginning (12% of given responses) or at the stop of the line (43% of given responses).

Put these fractions in ascending order

Children were asked to sort the post-obit numbers in ascending guild: 3/four, 1/2, 8/4, and one. 55% of 4th-graders placed 1 at the end of the sequence, later on 8/four. Furthermore, 22% of 4-graders placed ane at the beginning of the sequence, before 1/two and iii/iv. This mistake rate decreased in grades 5 and 6, just 30% of 6th-graders still put 1 at the stop of the sequence. These errors are consistent with the errors observed in the number line task. Children struggled with the relation betwixt fractions and the unit.

Comparison of fractions

Pupils had to choose which of two fractions was larger. There were three types of items: same denominators (Hateful = 83 ± 2%); same numerators (Mean = 56 ± 2%); and no common components (Mean = 65 ± 2%). An ANOVA on the type of fraction (3 levels: same denominators; same numerators; and no mutual components) revealed significant differences between types, F _{(2, 437)} = 1346.4, p < 0.001, η² _p = 0.90. Tukey mail service-hoc tests showed that scores for fractions with common denominators were higher than for fractions with common numerators (p < 0.001) and fractions with no common components (p < 0.001).

Operations

Performance for addition and subtraction with aforementioned denominators was improve than for addition and subtraction with unlike denominators (see Tabular array 5). This is not surprising equally addition and subtraction with unlike denominators are not yet part of the plan in Course iv. Only the procedure to find the lowest common denominator seems to pose issues in Grade 5 and 6. The most common error was based on the natural number bias, that is, calculation or subtracting numerators and denominators as if in that location were natural numbers (e.g., = one/3 + 1/4 = 2/vii). 62% of 4th-graders made this error for improver and subtraction with different denominators, and this percentage even so reached 22% in Grade 6. Surprisingly, performance for multiplication of fractions was amend in Form 4 than in Grade 5. An ANOVA showed meaning differences on the types of operations, F _{(2, 437)} = 135.five, p < 0.001, η² _p = 0.45. Tukey mail service-hoc tests showed that functioning was better for addition and subtraction with common denominators than for addition and subtraction with different denominators and multiplication (p < 0.001).

Table v. Mean percentage of right responses and standard deviation for each type of operations in Grade 4–six.

Simplification

As can exist seen in Table half dozen, operation in the simplification job was improve for fractions that could exist divided past ii (e.g., 4/8) than for fractions that could exist divided by 3 (e.g., 15/ix), F _{(1, 438)} = 384.iv, p < 0.001, η² _p = 0.64. In that location was no pregnant divergence between simplification of proper and improper fractions, fractions, F _{(ane, 438)} = one.76, p = 0.19.

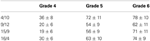
Table 6. Mean percentage of correct responses and standard difference for the simplification task in each grade.

Discussion

In this study, nosotros investigated the difficulties encountered by main school children when learning fractions. One of the primary goals of this study was to analyze the relationships between conceptual and procedural understanding of fractions. In order to do then, a test was administered in Form 4–six in classes of the French Community of Belgium. The test was based on the unlike conceptual meanings of fractions, namely part-whole/partition, number, proportion, as well as on procedural questions involving arithmetical operations and simplification of fractions.

Globally, the results showed big differences between categories. Pupils seemed to main the part-whole concept, whereas numbers and operations posed tremendous problems. Some conceptual meanings, such as numbers, were less used in chief school classes. Part-whole seems to be a concept that is widely used in the classrooms. Indeed, children performed well in the role-whole/sectionalisation category. Yet, they seem to have a stereotypic representation of fractions. Indeed, when they were asked to correspond a given fraction, they mostly used a circle or a square, even when drawing collections could have been easier (e.chiliad., 1/7). Moreover, when asked to select a figure representing a certain fraction, they performed ameliorate for continuous than discrete quantities. Pupils performed well with proportion items. These results contrast with textbooks and lessons given by teachers. In fact, the connection betwixt proportions and fractions is rarely made in textbooks and formal lessons, even if some aspects of fractions are based upon proportional reasoning (e.g., the rule of iii).

In the proportion category, most errors were linked to condiment reasoning. For example, when pupils are asked questions such as "3 cakes toll €12, 6 cakes cost €24, 8 cakes toll €?" the most mutual error would be the reply €36. In this case, children built their answer on only a subset of the given information and they practical additive strategies where multiplicative strategies should be used. Mistakes linked to condiment reasoning are usually reported during early stages of children's understanding of proportional reasoning (Lesh et al., 1988). This kind of mistakes was common in Course iv, but could however be observed in Grade 6.

Pupils performed poorly in the numerical category. Fifty-fifty if children are trained to deal with number lines from grade four, results showed major difficulties when they were asked to place a fraction on a graduated number line. They practise non seem to have an appropriate representation of the quantities of fractions. Other studies have reported that many pupils experience difficulties when asked to locate a fraction on a number line. Pupils often view the whole number line, irrespective of its magnitude as a single unit instead of a scale (Ni, 2001). When they are asked to place a fraction between 0 and 1, pupils often place fractions disregarding whatsoever other reference betoken or known fractions. Pearn and Stephens (2004) pointed out that the incorrect location of fractions could also be the consequence of a lack of accuracy when dividing segments.

The lack of accuracy in children's mental representations of the magnitude of fractions seems to be confirmed past the weak percentage of correct response for questions involving sorting out a range of fractions in ascending society. Furthermore, mean percent of correct responses for comparing of fractions were very low for fractions with common numerators and fractions no common components. When fractions share the same denominator (due east.g., 2/5_4/5), the global magnitude of fractions is congruent with the magnitude of the numerators (e.g., 4 is larger than two). In this case, pupils could only compare the numerators in order to choose the larger fraction. When fractions share the same numerator, the global magnitude of fractions is incongruent with the magnitude of denominators. Thus, pupils might non take the incongruity into account and their judgment might have been influenced past the whole number bias (Ni and Zhou, 2005). For fractions with no common components, pupils probably only compared numerators and denominators separately. This strategy led to larger error rates.

Focusing now on operations, children performed well in addition and subtraction of fractions with the aforementioned denominator, while functioning dropped dramatically in improver and subtraction of fractions with different denominators. The most common errors were dictated by the whole number bias (Ni and Zhou, 2005). For example, when asked 3/4 + 2/v = ?, the majority of pupils answers v/9. Surprisingly, results were poorer for items involving the multiplication of an integer by a fraction, than for multiplication of two fractions. In the last case, pupils could successfully use procedures based on natural numbers knowledge, which would explain higher percent of right response. Another surprising result was the better functioning in Grade four than Grade five when children were asked to multiply an integer by a fraction. There might be a contamination of procedures applied to addition and subtraction with different denominators learnt in Grade 5.

Results showed massive familiarity effects in every category. Children performed significantly improve on questions including familiar fractions, such every bit 1/2, ane/4, or 3/4 than on items with less familiar fractions. This could exist due to the fact that the magnitude of i/2 is known amend than other fractional magnitudes. Nosotros do not know precisely when children start to quantify continuous quantities in informal contexts. Bryant (1974) suggests that children are able to empathize part/office relations before office/whole relations. Relations such as "larger than/smaller than" and "equals to" could be the first logical relationships used at the beginning of fraction learning. Spinillo and Bryant (1991) designed experiments to analyse how iv- to 7-year-olds use the concept of "half" in equivalence judgment tasks. Their results suggest that using the concept of one-half would be the beginning step in relationships used past children to quantify fractions.

Desli (1999) besides investigated the role of one-half by examining function/whole relationships. 6- to eight-year-olds were told that two parties had been organized and that chocolate bars would exist equally distributed among children. They had to judge if they would receive the same corporeality of chocolate bars in both parties, and if non, in which party they would become more chocolate bars. Children had ceiling performance when they could use one-half as a reference. In the status where they could non use half equally a reference, only 8-yr-olds had functioning to a higher place gamble. Desli (1999) also showed the importance of the concept of one-half in the structure of fractions quantifications. In a recent study using a fraction-based judgment job, Mazzocco et al. (2013) showed that fractions equivalent to 1/2 were easier to anticipate. Moreover, children as young as iii and 4 years one-time already accept a practiced representation of the one-half boundary (Singer-Freeman and Goswami, 2001). As children are frequently exposed to 1/ii quite early on in life, the familiarity of that quantity might induce a different blazon of mental representations compared to other less familiar fractions. Pupils might benefit from lessons including a larger puddle of fractions. Pedagogy programs more often than not insist on quantities that tin can be divided by ii. This limited vision of fractions seems to generate difficulties when it comes to generalization. Teachers could diversify the number of fractions used during lessons.

Improper fractions represented some other major difficulty for primary school children (Bright et al., 1988; Tzur, 1999). The main difficulty appeared in the examination when pupils were asked to graphically represent an improper fraction or when an improper fraction was presented in an ordering chore. When pupils were asked to guild 1 in a sequence involving fractions, the most mutual error was to put it at the stop of the sequence, fifty-fifty if there was an improper fraction. This could mean that some children cannot imagine fractions can be larger than 1. This is consistent with the results found past Kallai and Tzelgov (2009) who showed that adults have a mental representation of what they called a "generalized fraction." A "generalized fraction corresponds to an "entity smaller than ane" emerging from the common note of fraction (Kallai and Tzelgov, 2009).

Furthermore, children seem to have a limited conception of the relation betwixt 1 and fractions. Looking at questions on number lines and the ordering job, nosotros observed ii different conceptions regarding the number i. In the first instance, i was put at the start of the sequence. This can exist interpreted equally 1 beingness at the beginning of counting sequence. This mistake is over again linked to the whole number bias (Ni and Zhou, 2005). Indeed, pupils based their answer on prior noesis and the expectation that fractions follow the same dominion of counting as whole numbers. In the 2d instance, one was placed at the end of the sequence. Children who made this fault considered fractions equally existence entities smaller than one.

Equivalent fractions were not understood by the majority of children (Kamii and Clark, 1995; Arnon et al., 2001). For example, performance was poor when they were asked to identify two/3 on a number line when the references were 0 and 1/6. Even so, their score was high for questions involving simplification of fraction. There was a articulate dissociation between conceptual and procedural understanding. Children mastered the procedure applied to simplify fractions, only did not seem to sympathise the underlying concept of equivalent fractions.

To sum up, the exam that we designed revealed many weaknesses in understanding fractions in primary schoolhouse. Teaching practice seems to focus more on procedures than on conceptual agreement of fractions. Just our results showed that procedures are not sufficient to behave out operations with fractions for instance. Fifty-fifty if pupils are intensively trained with finding the least common denominators procedure, the percentage of correct responses for addition and subtraction with different denominators remained low. Conceptual understanding is essential to ensure a deep agreement of fractions. In the U.Southward., it is already been recommend for the teaching of fractions (NCTM, 2000; Fazio and Siegler, 2012), and based on our results, we would suggest this recommendation should also utilise for the French Community of Belgium.

Nosotros argue that children might do good from a training based on concrete objects manipulation and explicit learning of rational numbers characteristics. Pedagogy children concrete activities could help them develop the corresponding abstract concepts (Arnon et al., 2001; Gabriel et al., 2012). For example, most primary school children consider fractions equally existence entities smaller than one (Behr et al., 1992; Stafylidou and Vosniadou, 2004). Moreover, most of them do not seem to understand equivalent fractions. These item characteristics plant the principal differences betwixt fractions and natural numbers. Pupils might benefit from more training with concrete objects to realize the necessary conceptual reorganisation and understand the properties of fractions. Another interesting finding of this study is that children performed better with familiar fractions. It could be interesting to introduce a larger variety also as diversified representations of fractions in lessons. By integrating a larger range of fractions, children might get a more than flexible representation of the magnitude of fractions.

Unfortunately, our experiment did not allow united states of america to describe conclusions on how conceptual and procedural knowledge influence each other. Correlation analysis revealed that every conceptual and procedural items were positively correlated with each other. Therefore, links between conceptual and procedural agreement are hard to interpret. This might hateful that both types of knowledge are not contained and could be every bit important when learning fractions. Both types of knowledge might evolve in an iterative fashion. Besides, individual differences accept been reported in the evolution of conceptual and procedural knowledge (Hallett et al., 2010; Hecht and Vagi, 2012). Children differ in the use of conceptual and procedural knowledge to solve fraction problems (Hallett et al., 2010). Some other reason tin can account for the difficulties to interpret findings obtained with a hypothetical measure of conceptual and procedural knowledge. The assessment of conceptual knowledge might reverberate, to some extent, procedural cognition and vice versa (Rittle-Johnson and Alibali, 1999). Future investigations are required to shed light on the links betwixt conceptual and procedural knowledge in fraction learning and examine the possible reasons for private differences.

In conclusion, our results showed that principal school children main the role-whole and proportion categories, but they struggle to understand fractions as numbers. Equivalent and improper fractions are very hard to grasp, and pupils seem to utilize procedures that they practice non really understand. This might be linked to teaching practice that allocates more time and exercises merely based on procedures.

Disharmonize of Interest Argument

The authors declare that the enquiry was conducted in the absence of any commercial or financial relationships that could be construed every bit a potential conflict of interest.

Acknowledgments

This enquiry was supported by a enquiry grant from the Service général du Pilotage du système éducatif du Ministère de la Communauté Française de Belgique to Alain Content, Vincent Carette, and Bernard Rey and a grant from the Wiener-Anspach Fund to Florence Gabriel. We thank the reviewers for their helpful and constructive comments. Professor Vincent Carette, who helped initiate this inquiry project, died suddenly in January 2011. We would like to dedicate this publication to his retentiveness.

References

Arnon, I., Nesher, P., and Nirenburg, R. (2001). Where practise fractions encounter their equivalents? Can this meet take place in elementary-school? Int. J. Comput. Math. Larn. half-dozen, 167–214. doi: 10.1023/A:1017998922475

CrossRef Full Text

Baroody, A. J. (2003). "The development of adaptive expertise and flexibility: the integration of conceptual and procedural knowledge," in The Development of Arithmetic Conceptsand Skills: Amalgam Adaptive ExpertiseI, eds A. J. Baroody and A. Dowker (Mahwah, NJ: Erlbaum), one–33.

Behr, Thou. J., Harel, Thou., Mail service, T., and Lesh, R. (1992). "Rational number, ratio, and proportion," in Handbook of Enquiry on Mathematics Teaching and Learning, ed D. A. Grouws (New York, NY: Macmillan), 296–333.

Behr, M. J., Lesh, R., Post, T. R., and Silverish, E. A. (1983). "Rational numbers concepts," in Acquisition of Mathematics Concepts and Processes, eds R. Lesh and 1000. Landau (New York, NY: Bookish Printing), 91–125.

Bonato, M., Fabbri, Southward., Umiltà, C., and Zorzi, M. (2007). The mental representation of numerical fractions: real or integer? J. Exp. Psychol. Hum. Percept. Perform. 33, 1410–1419. doi: 10.1037/0096-1523.33.6.1410

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Vivid, Grand., Behr, K., Mail, T., and Wachsmuth, I. (1988). Identifying fractions on number lines, J. Res. Math. Educ. xix, 215–232. doi: 10.2307/749066

CrossRef Total Text

Brissiaud, R. (1998). "Les fractions et les décimaux au CM1. Une nouvelle approche," in Actes du XXVème Colloque des Formateurs et Professeurs de Mathématiques chargés de la Germination des Maîtres, (IREM de Brest), 147–171.

Brousseau, G., Brousseau, N., and Warfield, Five. (2004). Rationals and decimals as required in the schoolhouse curriculum. Part ane: rationals as measurements. J. Math. Behav. 23, one–twenty. doi: ten.1016/j.jmathb.2003.12.001

CrossRef Full Text

Bryant, P. (1974). Perception and Agreement in Young Children: An Experimental Approach, Vol. 588. London: Methuen.

Byrnes, J. P., and Wasik, B. A. (1991). Function of conceptual cognition in mathematical procedural learning. Dev. Psychol. 27, 777–786. doi: 10.1037/0012-1649.27.v.777

CrossRef Total Text

Charalambous, C., and Pitta-Pantazi, D. (2007). Drawing on a theoritical model to written report students' understandings of fractions. Educ. Stud. Math. 64, 293–316. doi: ten.1007/s10649-006-9036-2

CrossRef Full Text

Coquin-Viennot, D., and Camos, V. (2006). "Décimaux et fractions," in La noesis mathématique chez l'enfant, eds P. Barrouillet and V. Camos (Marseille: Solal), 145–154.

Desli, D. (1999). Children's Understanding of Intensive Quantities. Unpublished PhD thesis. Institute of Instruction, University of London.

Fazio, 50., and Siegler, R. (2012). Didactics fractions. Educ. Pract. Ser. 22, 1–28.

Gabriel, F., Coché, F., Szucs, D., Carette, 5., Rey, B., and Content, A. (2012). Developing children's agreement of fractions: an intervention written report. Mind Encephalon Educ. 6, 137–146. doi: 10.1111/j.1751-228X.2012.01149.ten

CrossRef Full Text

Gelman, R., and Williams, E. M. (1997). "Enabling constraints for cognitive development and learning: domain specificity and epigenesist," in Cognitive Development, Handbook of Kid Psychology, fifth Edn, eds D. Kuhn and R. Siegler (New York, NY: Wiley), 575–630.

Grégoire, J. (2008). Aux Sources des Difficultés de L'apprentissage des Fractions. Brussels: Seminar given at, Université Libre de Bruxelles.

Grégoire, J., and Meert, Grand. (2005) "L'apprentissage des nombres rationnels et ses obstacles," in Les Troubles Du Calcul, ed M.-P. Noël (Marseille: Solal), 223–251.

Halford, G. Southward. (1993). Children'southward Understanding: The Development of Mental Models. Hillsdale, NJ: Erlbaum.

Hallett, D., Nunes, T., and Bryant, P. (2010). Individual differences in conceptual and procedural noesis when learning fractions. J. Educ. Psychol. 102, 395–406. doi: 10.1037/a0017486

CrossRef Total Text

Hiebert, J. (ed.). (1986). Conceptual and Procedural Cognition: the Case of Mathematics. Hillsdale, NJ: Erlbaum.

Hiebert, J., and Lefevre, P. (1986). "Conceptual and procedural knowledge in mathematics: an introductory analysis," in Conceptualand Procedural Cognition: the Case of Mathematics, ed J. Hiebert (Hillsdale, NJ: Lawrence Erlbaum Associates), ane–27.

Kallai, A., and Tzelgov, J. (2009). A generalized fraction: an entity smaller than 1 on the mental number line. J. Exp. Psychol. Hum. Percept. Perform. 35, 1845–1864. doi: ten.1037/a0016892

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kamii, C., and Clark, F. B. (1995). Equivalent fractions: their difficulty and educational implications. J. Math. Behav. xiv, 365–378. doi: 10.1016/0732-3123(95)90035-7

CrossRef Full Text

Kerslake, D. (1986). Fractions: Children's Strategies and Errors. A Report of the Strategies and Errors in Secondary Mathematics Project. England: NFER-NELSON Publishing Visitor, Ltd.

Kieren, T. E. (1976). "On the mathematical, cognitive, and instructional foundations of rational numbers," in Number and Measurement: Papers from a Research Workshop, ed R. Lesh (Columbus, OH: ERIC/SMEAC), 101–144.

Kieren, T. E. (1988) "Personal knowledge of rational numbers: its intuitive and formal development," in Research Agenda for Mathematics Education: Number Concepts and Operations in the Center Grades, Vol. ii, eds J. Hiebert and M. Behr (Virginia: Lawrence Erlbaum), 162–181.

Kieren, T. E. (1993). "Rational and Partial Numbers: From Quotient fields to Recursive understanding," in Rational Numbers: An Integration of Research, eds T. P. Carpenter, East. Fennema, and T. A. Romberg (Hillsdale, NJ: Erlbaum), 49–84.

Lesh, R., Post, T., and Behr, Chiliad. (1988). "Proportional reasoning," in Number Concepts and Operations in the Heart Grades, eds J. Hiebert and G. Behr (Reston, VA: Lawrence Erlbaum and National Council of Teachers of Mathematics), 93–118.

Mamede, E., Nunes, T., and Bryant, P. (2005). "The equivalence and ordering of fractions in office-whole and caliber situations," in PME CONFERENCE, Vol. 29, 3.

Mazzocco, Yard. 1000. M., Myers, G. F., Lewis, Thousand. Due east., Hanich, 50. B., and Irish potato, M. M. (2013). Limited knowledge of fraction representations differentiates eye school students with mathematics learning disability (dyscalculia) vs. depression mathematics achievement. J. Exp. Kid Psychol. 115, 371–387. doi: 10.1016/j.jecp.2013.01.005

Pubmed Abstract | Pubmed Total Text | CrossRef Full Text

Ministère de la Communauté française, (1999). Socles de Compétences Enseignement Fondamental et Premier degré de l'enseignement Secondaire. Test de Mathématique, Résultats et Commentaires. Bruxelles: Administration générale de fifty'Enseignement et de la Recherche scientifique.

Moss, J., and Case, R. (1999). Developing children'southward understanding of the rational numbers: a new model and an experimental curriculum. J. Res. Math. Educ. thirty, 122–147. doi: ten.2307/749607

CrossRef Total Text

National Council of Teachers of Mathematics. (2000). Principles and Standards for Schoolhouse Mathematics. Reston, VA: writer.

Ni, Y. (2000). How valid is information technology to utilise number lines to measure children's conceptual cognition virtually rational number. Educ. Psychol. 20, 139–152. doi: 10.1080/713663716

CrossRef Total Text

Ni, Y., and Zhou, Y. D. (2005). Didactics and learning fraction and rational numbers: the origins and implications of whole number bias. Educ. Psychologist xl, 27–52. doi: x.1207/s15326985ep4001_3

CrossRef Full Text

Nunes, T., and Bryant, P. (1996). Children Doing Mathematics. Oxford: Blackwell.

Pearn, C., and Stephens, M. (2004). "Why you take to probe to find what year 8 students actually recall about fractions," in Newspaper Presented at the Mathematics Education for the Third Millennium: Towards 2010, (Townsville).

Rittle-Johnson, B., Siegler, R. Southward., and Alibali, M. W. (2001). Developing conceptual agreement and procedural skill in mathematics: an iterative process. J. Educ. Psychol. 93, 346–362. doi: 10.1037/0022-0663.93.2.346

CrossRef Full Text

Rittle-Johnson, B., and Alibali, K. W. (1999). Conceptual and procedural cognition of mathematics: does 1 lead to the other? J. Educ. Psychol. 91, 175–189. doi: 10.1037/0022-0663.91.ane.175

CrossRef Total Text

Rouche, Northward. (1998). L'esprit des Sciences. Pourquoi ont-ils Inventé les Fractions? Paris: Ellipses.

Schneider, M., and Stern, Eastward. (2005). "Conceptual and procedural cognition of a mathematics problem: their measurement and their causal interrelations," in Paper Presented at the 27th Almanac Meeting of the Cognitive Science Lodge (CSS), (Stresa).

Singer-Freeman, Thousand. Due east., and Goswami, U. (2001). Does one-half a pizza equal one-half a box of chocolates?: proportional matching in an analogy chore. Cogn. Dev. 16, 811–829. doi: 10.1016/S0885-2014(01)00066-1

CrossRef Full Text

Spinillo, A. G., and Bryant, P. (1991). Children'south proportional judgments: The importance of "one-half". Child Dev. 62, 427–440. doi: 10.1111/j.1467-8624.1991.tb01542.ten

CrossRef Full Text

Stafylidou, Due south., and Vosniadou, S. (2004). The development of students' understanding of the numerical value of fractions. Learn. Instr. 14, 503–518. doi: 10.1016/j.learninstruc.2004.06.015

CrossRef Full Text

Tzur, R. (1999). An integrated study of children's structure of improper fractions and the teacher'due south role in promoting that learning. J. Res. Math. Educ. 30, 390–416. doi: ten.2307/749707

CrossRef Total Text

Vamvakoussi, Ten., and Vosniadou, S. (2004). Understanding the structure of the ready of rational numbers: a conceptual change approach, Learn. Instr. 14, 453–467. doi: ten.1016/j.learninstruc.2004.06.013

CrossRef Total Text

Appendix

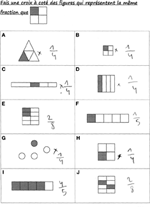
Figure A1. Office-whole item: select fractions representing the same fraction as 1/4. To get full marks, children had to select panels (A,B,D,Due east,Thou,H) and (J). In this item example, the student failed to spot fractions equivalence.

babcockwhipmed.blogspot.com

Source: https://www.frontiersin.org/articles/10.3389/fpsyg.2013.00715/full

Share this post